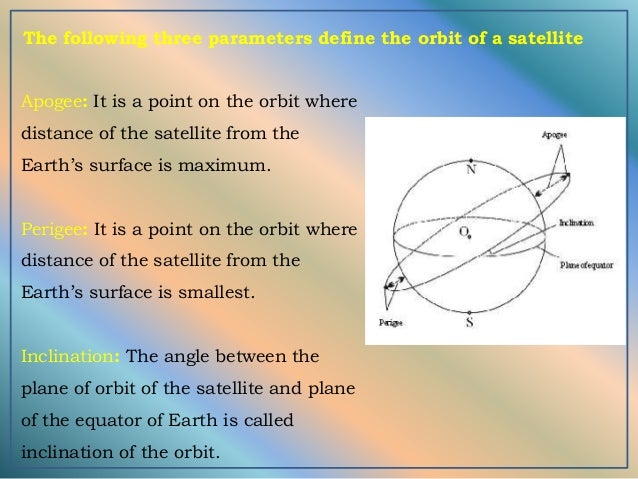
- Sun Synchronous Orbit Inclination Vs Altitude
- Sun Synchronous Definition
- Sun Synchronous Satellite
- Sun Synchronous Satellite
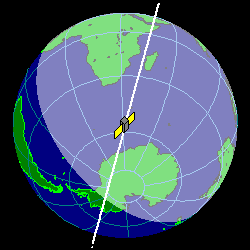
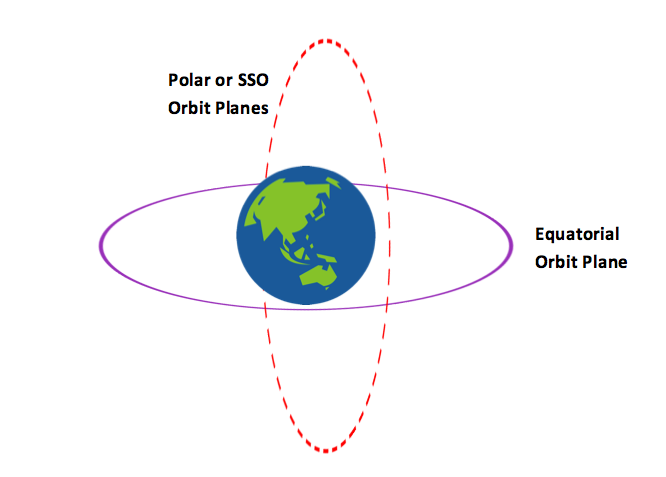
A sun-synchronous orbit (SSO), also called a heliosynchronous orbit,[1] is a nearly polar orbit around a planet, in which the satellite passes over any given point of the planet's surface at the same local mean solar time.[2][3] More technically, it is an orbit arranged so that it precesses through one complete revolution each year, so it always maintains the same relationship with the Sun. A Sun-synchronous orbit is useful for imaging, spy, and weather satellites,[4] because every time that the satellite is overhead, the surface illumination angle on the planet underneath it will be nearly the same.
Applications[edit]
(Of a satellite or its orbit) passing over the same points on the earth’s (or other planet’s) surface at the same times each day. – Initial performance to sun-synchronous orbit (800 km.): more than 5.5 metric tons. A64: with four solid rocket motors – Initial performance to geostationary transfer orbit: 11 metric tons with growth potential – Initial performance to geostationary transfer orbit (GTO+, 2,200 km. Perigee): 9.3 metric tons. Define sun-synchronous orbit. Sun-synchronous orbit synonyms, sun-synchronous orbit pronunciation, sun-synchronous orbit translation, English dictionary definition of sun-synchronous orbit. An orbit in which the satellite's orbital plane is at a fixed orientation to the sun, i.e., the orbit precesses about the earth at the same rate that the. A Sun-synchronous orbit (sometimes called a heliosynchronous orbit 1) is a geocentric orbit which combines altitude and inclination in such a way that an object on that orbit will appear to orbit in the same position, from the perspective of the Sun, during its orbit around the Earth. More technically, it is an orbit arranged in such a way that it precesses once a year. This video illustrates the principle of Sun-synchronous orbits used by EUMETSAT's Metop satellites. The satellite's orbital plane is indicated by the red tor.
A Sun-synchronous orbit is useful for imaging, spy, and weather satellites,[4] because every time that the satellite is overhead, the surface illumination angle on the planet underneath it will be nearly the same. This consistent lighting is a useful characteristic for satellites that image the Earth's surface in visible or infrared wavelengths, such as weather and spy satellites; and for other remote-sensing satellites, such as those carrying ocean and atmospheric remote-sensing instruments that require sunlight. For example, a satellite in Sun-synchronous orbit might ascend across the equator twelve times a day each time at approximately 15:00 mean local time.
Special cases of the Sun-synchronous orbit are the noon/midnight orbit, where the local mean solar time of passage for equatorial latitudes is around noon or midnight, and the dawn/dusk orbit, where the local mean solar time of passage for equatorial latitudes is around sunrise or sunset, so that the satellite rides the terminator between day and night. Riding the terminator is useful for active radar satellites, as the satellites' solar panels can always see the Sun, without being shadowed by the Earth. It is also useful for some satellites with passive instruments that need to limit the Sun's influence on the measurements, as it is possible to always point the instruments towards the night side of the Earth. The dawn/dusk orbit has been used for solar-observing scientific satellites such as Yohkoh, TRACE, Hinode and PROBA2, affording them a nearly continuous view of the Sun.
Orbital precession[edit]
A Sun-synchronous orbit is achieved by having the osculating orbital plane precess (rotate) approximately one degree eastward each day with respect to the celestial sphere to keep pace with the Earth's movement around the Sun.[5] This precession is achieved by tuning the inclination to the altitude of the orbit (see Technical details) such that Earth's equatorial bulge, which perturbs inclined orbits, causes the orbital plane of the spacecraft to precess with the desired rate. The plane of the orbit is not fixed in space relative to the distant stars, but rotates slowly about the Earth's axis.

Typical Sun-synchronous orbits around Earth are about 600–800 km in altitude, with periods in the 96–100-minute range, and inclinations of around 98°. This is slightly retrograde compared to the direction of Earth's rotation: 0° represents an equatorial orbit, and 90° represents a polar orbit.[5]
Sun-synchronous orbits are possible around other oblate planets, such as Mars. A satellite orbiting a planet such as Venus that is almost spherical will need an outside push to maintain a Sun-synchronous orbit.
Technical details[edit]
The angular precession per orbit for an Earth orbiting satellite is given by
where
- J2 is the coefficient for the second zonal term (1.08263×10−3) related to the oblateness of the Earth (see geopotential model),
- RE is the mean radius of the Earth, roughly 6378km
- p is the semi-latus rectum of the orbit,
- i is the inclination of the orbit to the equator.
An orbit will be Sun-synchronous when the precession rate ρ equals the mean motion of the Earth about the Sun, which is 360° per sidereal year (1.99096871×10−7rad/s), so we must set ΔΩ/T = ρ, where T is the orbital period.
As the orbital period of a spacecraft is
where a is the semi-major axis of the orbit and μ is the standard gravitational parameter of the planet (398600.440 km3/s2 for Earth); as p ≈ a for a circular or almost circular orbit, it follows that
or when ρ is 360° per year,
As an example, for a = 7200 km (the spacecraft about 800 km over the Earth surface) one gets with this formula a Sun-synchronous inclination of 98.696°.
Note that according to this approximation cos i equals −1 when the semi-major axis equals 12352 km, which means that only smaller orbits can be Sun-synchronous. The period can be in the range from 88 minutes for a very low orbit (a = 6554 km, i = 96°) to 3.8 hours (a = 12352 km, but this orbit would be equatorial with i = 180°). A period longer than 3.8 hours may be possible by using an eccentric orbit with p < 12352 km but a > 12352 km.
If one wants a satellite to fly over some given spot on Earth every day at the same hour, it can do between 7 and 16 orbits per day, as shown in the following table. (The table has been calculated assuming the periods given. The orbital period that should be used is actually slightly longer. For instance, a retrograde equatorial orbit that passes over the same spot after 24 hours has a true period about 365/364 ≈ 1.0027 times longer than the time between overpasses. For non-equatorial orbits the factor is closer to 1.)
| Orbits per day | Period (h) | Height above Earth's surface (km) | Maximal latitude | Incli- nation | |
|---|---|---|---|---|---|
| 16 | 1+1/2 | = 1:30 | 000274 | 83.4° | 096.6° |
| 15 | 1+3/5 | = 1:36 | 000567 | 82.3° | 097.7° |
| 14 | 1+5/7 | ≈ 1:43 | 000894 | 81.0° | 099.0° |
| 13 | 1+11/13 | ≈ 1:51 | 001262 | 79.3° | 100.7° |
| 12 | 2 | 001681 | 77.0° | 103.0° | |
| 11 | 2+2/11 | ≈ 2:11 | 002162 | 74.0° | 106.0° |
| 10 | 2+2/5 | = 2:24 | 002722 | 69.9° | 110.1° |
| 09 | 2+2/3 | = 2:40 | 003385 | 64.0° | 116.0° |
| 08 | 3 | 004182 | 54.7° | 125.3° | |
| 07 | 3+3/7 | ≈ 3:26 | 005165 | 37.9° | 142.1° |
When one says that a Sun-synchronous orbit goes over a spot on the Earth at the same local time each time, this refers to mean solar time, not to apparent solar time. The Sun will not be in exactly the same position in the sky during the course of the year (see Equation of time and Analemma).
Sun Synchronous Orbit Inclination Vs Altitude
Sun-synchronous orbits are mostly selected for Earth observation satellites, with an altitude typically between 600 and 1000 km over the Earth surface. Even if an orbit remains Sun-synchronous, however, other orbital parameters such as argument of periapsis and the orbital eccentricity will evolve, due to higher order perturbations in the Earth's gravitational field, the pressure of sunlight, and other causes. Earth observation satellites, in particular, prefer orbits with constant altitude when passing over the same spot. Careful selection of eccentricity and location of perigee reveals specific combinations where the perturbations largely cancel and hence the orbit is relatively stable – a frozen orbit. The ERS-1, ERS-2 and Envisat of European Space Agency, as well as the MetOp spacecraft of EUMETSAT and RADARSAT-2 of the Canadian Space Agency, are all operated in such Sun-synchronous frozen orbits.[6]
See also[edit]
References[edit]
- ^Tscherbakova, N. N.; Beletskii, V. V.; Sazonov, V. V. (1999). 'Stabilization of heliosynchronous orbits of an Earth's artificial satellite by solar pressure'. Cosmic Research. 37 (4): 393–403. Bibcode:1999KosIs..37..417S.
- ^'SATELLITES AND ORBITS'(PDF).
- ^'Types of Orbits'. marine.rutgers.edu. Retrieved 2017-06-24.
- ^ abOur Changing Planet: The View from Space (1st ed.). Cambridge University Press. 2007. pp. 339. ISBN978-0521828703.
- ^ abRosengren, M. (November 1992). 'ERS-1 - An Earth Observer that exactly follows its Chosen Path'. ESA Bulletin (72). Bibcode:1992ESABu..72...76R.
- ^Rosengren, Mats (1989). 'Improved technique for Passive Eccentricity Control (AAS 89-155)'. Advances in the Astronautical Sciences. 69. AAS/NASA. Bibcode:1989ommd.proc...49R.
Further reading[edit]
- Sandwell, David T., The Gravity Field of the Earth - Part 1 (2002) (p. 8)
- Sun-Synchronous Orbit dictionary entry, from U.S. Centennial of Flight Commission
- Boain, Ronald J. (February 2004). 'The A-B-Cs of Sun Synchronous Orbit Design'(PDF). Space Flight Mechanics Conference. Archived from the original(PDF) on 2007-10-25.
External links[edit]

Sun Synchronous Definition
What would happen if the Earth stopped spinning?
The probability for such an event is practically zero in the next few billion years. If the Earth stopped spinning suddenly, the atmosphere would still be in motion with the Earth's original 1100 mile per hour rotation speed at the equator. All of the land masses would be scoured clean of anything not attached to bedrock. This means rocks, topsoil, trees, buildings, your pet dog, and so on, would be swept away into the atmosphere.
If the process happened gradually over billions of years, the situation would be very different, and it is this possibility which is the most likely as the constant torquing of the Sun and Moon upon the Earth finally reaches it's conclusion. If the rotation period slowed to 1 rotation every 365 days a condition called 'sun synchronous', every spot in the Earth would have permanent daytime or nighttime all year long. This is similar to the situation on the Moon where for 2 weeks the front-side is illuminated by the Sun, and for 2 weeks the back side is illuminated. This situation for the Earth is not the condition of 'stopped' rotation, but it is as close as the laws of physics will let the Earth get.
Sun Synchronous Satellite
If it stopped spinning completely...not even once every 365 days, you would get 1/2 year daylight and 1/2 year nightime. During daytime for 6 months, the surface temperature would depend on your latitude, being far hotter that it is now at the equator than at the poles where the light rays are more slanted and heating efficiency is lower. This long-term temperature gradient would alter the atmospheric wind circulation pattern so that the air would move from the equator to the poles rather than in wind systems parallel to the equator like they are now. The yearly change in the Sun's position in the sky would now be just its seasonal motion up and down the sky towards the south due to the orbit of the Earth and its axial tilt. As you moved along constant lines of Earth latitude, you would see the elevation of the Sun increase or decrease in the sky just as we now see the elevation of the Sun change from a single point on the Earth due to the Earth's daily rotation.
For example, if you were at a latitude of +24 degrees North in the Summer and at a longitude where the Sun was exactly overhead, it would slide gradually to the horizon as Fall approached, but since the Sun has moved 90 degrees in its orbit, it would now be due west. Then as we approach Winter, you would now be located on the dark side of the Earth, and would have to travel in longitude to a location 180 degrees around the Earth to see the Sun 1/2 way up the sky because in the Winter, the Sun is 48 degrees south of its summer location in the sky. It's a little confusing, but if you use a globe of the Earth and orient it the right way, you can see how all this works out.
As for other effects, presumably the magnetic field of the Earth is generated by a dynamo effect that involves its rotation. If the Earth stopped rotating, it's magnetic field would no longer be regenerated and it would decay away to some low, residual value due to the very small component which is 'fossilized' in its iron-rich rocks. There would be no more 'northern lights' and the Van Allen radiation belts would probably vanish, as would our protection from cosmic rays and other high-energy particles. This is a significant biohazard.
Sun Synchronous Satellite
Copyright 1997 Dr. Sten Odenwald
Return to Ask the Astronomer.
